As análises ou interpretações dos resultados geram HIPÓTESES, que
precisam ser confirmadas com mais dados ou pela interpretação de humanos
(geralmente analisando eventos da vida real).
Exemplo: um gráfico mostrando subida nas vendas. Procurar o porquê. A resposta
pode estar em ações feitas fora da empresa (e não documentadas ou registradas
com dados).
ISTO NÃO É UM CUBO
Isto é um cubo, pois há um atributo na linha e outro na coluna.
Unidades Vendidas
Observações:
Cliente A: vem diminuindo as compras
Cliente B deixou de comprar
Cliente C irregular ou sazonal, ver caraterística dos anos em que
comprou
Cliente D teve uma entressafra
Uma representação gráfica facilita muita esta visualização
O que analisar:
- picos (subidas ou descidas que se destacam do resto) e procurar
investigar por que os picos ocorreram;
- linhas retas (comportamento normal): é bom também saber o que
funciona sem desvios ou exceções;
- identificar padrões sazonais, ou seja, repetições em épocas
específicas (mês, duplas ou trios de meses, dia da semana); exemplo: picos que
acontecem especificamente em certos momentos (a cada 4 anos, vendas de TVs
sobem muito)
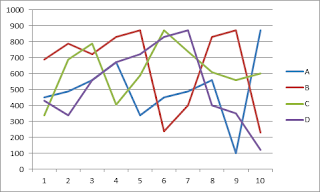
Abaixo temos um cubo típico: um atributo na linha (com valores de 1 a
10) e outro atributo nas colunas (com valores de A a D).
Imagine que os valores na linha ou na coluna são faixas de idades. Não
use valores absolutos, porque para encontrar padrões precisamos ter repetições.
Usando valores absolutos (exemplo, idade, quantidade, valor), talvez haja
poucas repetições. Então faça discretização, ou seja, crie faixas de valores
que as chances de repetição são maiores.
|
A
|
B
|
C
|
D
|
1
|
450
|
690
|
340
|
430
|
2
|
490
|
789
|
450
|
340
|
3
|
560
|
405
|
490
|
450
|
4
|
670
|
590
|
560
|
720
|
5
|
720
|
456
|
100
|
830
|
6
|
830
|
1020
|
870
|
870
|
7
|
870
|
720
|
740
|
239
|
8
|
740
|
830
|
610
|
400
|
9
|
610
|
870
|
560
|
349
|
10
|
490
|
230
|
600
|
120
|
No caso de produtos, podemos usar atributos tais como: classe, tipo,
setor ou categoria do produto; faixas de preços; frete grátis ou não; cor,
voltagem, marca, tipo de embalagem.
No caso de clientes, usar atributos tais como: cidade, bairro, sexo,
idade, classe social, nível de escolaridade.
No caso de vendas: faixa de valor total pago, forma de pagamento, loja,
vendedor,
O atributo data é clássico mas tem que separar em ano, mês, dia do mês
e dia da semana)
Se for usar hora, não utilizar os minutos (para aumenta repetições).
Uma boa também é usar turno (melhor que hora, pois haverá mais repetições).
Obs: não uso atributos onde haja um valor que domine. Por exemplo, se
pegar uma base de clientes e a grande maioria for da mesma cidade, não vale a
pena analisar o atributo cidade.
Podemos também usar valores binários.
Exemplo: comprou ou não nos últimos 6 meses. É claro que no ETL teremos
que criar tais valores, pois provavelmente deve aparecer data da compra.
Outros exemplos: tem interessem em ...; já comprou produto no setor X;
|
SIM
|
NÃO
|
1
|
450
|
690
|
2
|
490
|
789
|
3
|
560
|
405
|
4
|
670
|
590
|
5
|
720
|
456
|
6
|
830
|
1020
|
7
|
870
|
720
|
8
|
740
|
830
|
9
|
610
|
870
|
10
|
490
|
230
|
Ou criar escalas tipo:
|
SEMPRE
|
VÁRIAS VEZES
|
REGULARMENTE
|
RARAMENTE
|
NUNCA
|
1
|
450
|
690
|
340
|
430
|
239
|
2
|
490
|
789
|
450
|
340
|
400
|
3
|
560
|
405
|
490
|
450
|
349
|
4
|
670
|
590
|
560
|
720
|
120
|
5
|
720
|
456
|
100
|
830
|
490
|
6
|
830
|
1020
|
870
|
870
|
560
|
7
|
870
|
720
|
740
|
239
|
590
|
8
|
740
|
830
|
610
|
400
|
456
|
9
|
610
|
870
|
560
|
349
|
1020
|
10
|
490
|
230
|
600
|
120
|
720
|
UM CUBO COM 3 DIMENSÕES
|
|
A
|
B
|
C
|
D
|
E
|
X
|
1
|
450
|
690
|
340
|
430
|
239
|
|
2
|
490
|
789
|
450
|
340
|
400
|
|
3
|
560
|
405
|
490
|
450
|
349
|
Y
|
4
|
670
|
590
|
560
|
720
|
120
|
|
5
|
720
|
456
|
100
|
830
|
490
|
|
6
|
830
|
1020
|
870
|
870
|
560
|
|
7
|
870
|
720
|
740
|
239
|
590
|
Z
|
8
|
740
|
830
|
610
|
400
|
456
|
|
9
|
610
|
870
|
560
|
349
|
1020
|
|
10
|
490
|
230
|
600
|
120
|
720
|
É uma forma de representar 3 dimensões em duas (2 planos, pois não
temos a profundidade, a não ser que existissem monitores 3D).
Nas linhas, temos duas dimensões (2 atributos): um com valores X, Y e
Z, e outro atributo “interno” com os valores de 1 a 10.
Exemplos:
Países e tipos de cidades (ou tamanhos)
Lojas e vendedores
Setores e tipos de produtos
Marcas de produtos e faixas de valores
Isto é o que permite fazer drill-down e drill-up (subir ou descer na
hierarquia, ou seja, aumentar ou diminuir granularidade ou detalhes).
CIDADES E BAIRROS
Às vezes é difícil repetir valores para este tipo de atributo.
Então usar algum tipo de classificação, por exemplo:
grandes X pequenas
interior X capital
interior X litoral
renda da cidade ou índices sociais (tipo IDH, renda per capita média).
DOIS CUBOS DIFERENTES PARA COMPARAR
O melhor para compara é utilizar gráficos. 2 gráficos são mais fáceis
de comparar que 3, 4, etc. Mas podemos usar mais gráficos também.
Os cubos poderiam ser:
- períodos de tempos diferentes (ano X ano, mês X mês), para
compras/vendas/produção de clientes/vendedores/lojas/produtos ao longo do
tempo;
Ex. de descoberta: produto A (azul) foi adquirido regularmente ao longo
do tempo na amostra 1 com pequeno aclive no momento 7 (pode ser mês ou ano ou
dia da semana). Na 2ª amostra, o produto
vendeu de forma irregular ao longo do tempo (investigar por que as quedas e
subidas).
- vendas correlacionando tipo de produto X tipo de cliente
Ex. de descoberta: produto B (vermelho) foi mais adquirido por clientes
tipo 6 na amostra 1. Já na amostra 2, o mesmo produto foi o menos adquirido
pelo mesmo tipo de clientes.
Observação:
Gráficos em linha são melhores para analisar ritmo ou distribuição ao
longo do tempo, pois fica mais fácil ver subidas e descidas.
Gráficos com barras são melhores para comparar valores (quem está acima
de quem, altos X baixos).
Gráficos em Pizza são melhores para comparar proporções (onde valores
absolutos não são tão importantes).
Exemplo: qual setor gasta mais que os outros em termos %
(proporcionais).
Como nos gráficos abaixo.
Exemplo: gastos por setor (cada amostra é uma filial diferente; A x B).
Ex. de descoberta: setor roxo (valor 4) mantém proporção em ambas
amostras. Mas o setor 10 (lilás) é bem diferente de uma amostra para outra (18%
para 4%).
CRIAR SUBGRUPOS E COMPARAR
Subgrupos são amostras diferentes.
Exemplos:
- períodos de tempos
- subconjuntos extraídos de um valor único (ex. pegar somente pessoas
do sexo masculino, somente cidades com mais de 100 mil habitantes)ou com um
critério específico (ex. somente produtos com maior saída ou preço acima de
tanto).
Comparar:
- subgrupos entre si;
- comportamento do subgrupo X todo
MÉTRICAS OU MEDIDAS
O tipo de dado colocado dentro do cubo é chamado de métrica
ou medida.
Que dado ou atributo colocar dentro do cubo ?
Imagine que você está analisando diferentes tipos de
clientes. Uma medida seria avaliar a quantidade de produtos adquiridos por cada
tipo (ou por cada cliente especificamente). Entretanto, lucratividade é mais
importante que quantidade. Então talvez seja melhor utilizar como medida a soma
de valores gastos (ou lucro, que é igual receita menos despesa/custo).
Pode-se também utilizar média, máximo, mínimo, etc.
|
A
|
B
|
C
|
D
|
|
1
|
450
|
690
|
340
|
430
|
|
2
|
490
|
789
|
450
|
340
|
|
3
|
560
|
405
|
490
|
450
|
|
4
|
670
|
590
|
560
|
720
|
|
5
|
720
|
456
|
100
|
830
|
|
6
|
830
|
1020
|
870
|
870
|
|
7
|
870
|
720
|
740
|
239
|
|
8
|
740
|
830
|
610
|
400
|
|
9
|
610
|
870
|
560
|
349
|
|
10
|
490
|
230
|
600
|
120
|
Num hospital, talvez seja interessante analisar o número de
casos de uma doença (cruzando por exemplo, região X faixa etária). Mas também
podemos utilizar como medida a média de tempo de internação (cruzando por
exemplo, doença X sexo).
|
Masc
|
Fem
|
|
Grupo 1
|
15
|
6
|
|
Grupo 2
|
23
|
14
|
|
Grupo 3
|
5
|
40
|
|
Grupo 4
|
6
|
7
|
|
|
|
|
|
|
|
|
No exemplo acima, podemos ver claramente que as doenças dos
grupos 1 e 2 exigem maior tempo de internação para homens (quase o dobro de
dias que as mulheres). Já o grupo 3 inverte a gangorra, com 8x mais tempo para
mulheres que homens. E no grupo 4 há uma equilíbrio entre sexos.
Numa escola, a medida pode ser a nota tirada pelo aluno
(média) ou a contagem de vezes que o aluno recebeu alguma notificação negativa.
|
A
|
B
|
C
|
D
|
|
1
|
0
|
0
|
0
|
0
|
|
2
|
3
|
0
|
10
|
0
|
|
3
|
2
|
0
|
6
|
0
|
|
4
|
0
|
0
|
0
|
0
|
|
5
|
0
|
0
|
5
|
12
|
|
6
|
0
|
0
|
4
|
8
|
|
7
|
0
|
0
|
0
|
0
|
|
8
|
0
|
0
|
0
|
0
|
|
9
|
0
|
0
|
0
|
0
|
|
10
|
0
|
0
|
0
|
0
|
No cubo acima, as notas estão nas linhas e as colunas
representam níveis escolares diferentes (A menor nível, D o maior). Foi
utilizada como medida o número de alunos que receberam notificações negativas. Isto
significa que, no entroncamento da linha referente à nota 2 com a coluna
referente ao nível A, 3 alunos receberam notificações, ou seja, 3 alunos do
nível A receberam notificações e ficaram com nota 2.
Vejam que alunos aprovados (com notas igual ou maior que 7)
não receberam notificações em nenhum nível. No nível B, nenhum aluno recebeu
notificação (estudar por quê). Pelas análise das turmas A e C pode-se ver que
há uma escala: mais notificações para alunos com menos notas. E a turma do
nível D possui algo de interessante que é um grande número de notificações mas
para alunos que quase foram aprovados.